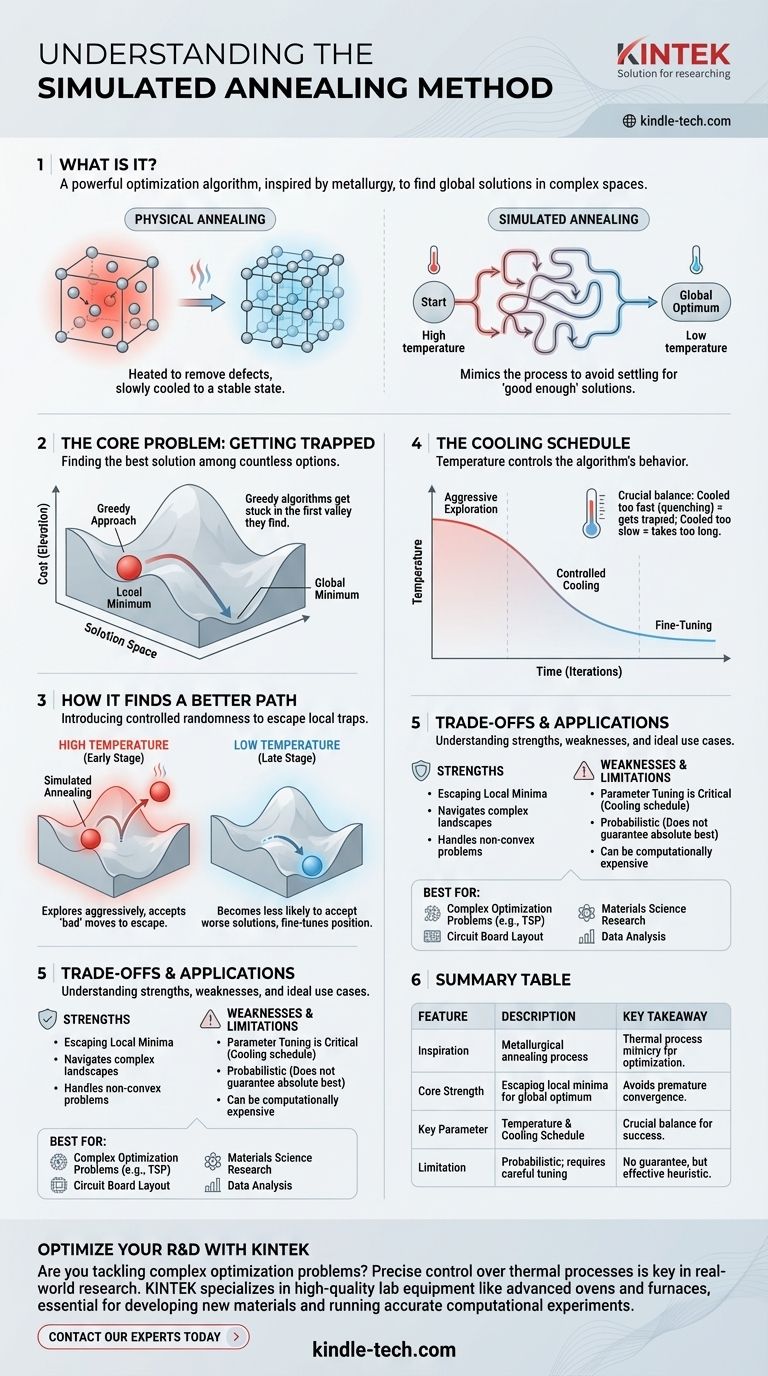
간단히 말해, 시뮬레이티드 어닐링(Simulated annealing)은 방대하고 복잡한 탐색 공간에서 좋은 (그리고 종종 전역적인) 해를 찾기 위해 사용되는 강력한 최적화 알고리즘입니다. 이는 야금학적 어닐링 과정에서 영감을 직접적으로 받았는데, 이 과정에서는 재료를 가열한 다음 천천히 냉각하여 결함을 제거하고 안정적인 저에너지 결정 상태에 도달하게 합니다. 이 알고리즘은 이러한 물리적 과정을 모방하여 추상적인 계산 문제를 해결합니다.
본질적으로 시뮬레이티드 어닐링은 금속 어닐링의 물리적 과정을 모방하여 "충분히 좋은" 해에 안주하는 일반적인 함정을 피합니다. 이는 광범위한 가능성을 탐색하는 것(고온)으로 시작하여 점차적으로 고품질의 안정적인 해(저온)에 초점을 맞춥니다.

핵심 문제: 갇히는 것
시뮬레이티드 어닐링을 이해하려면 먼저 이 알고리즘이 해결하는 문제, 즉 수많은 옵션 중에서 가능한 최상의 해를 찾는 최적화 작업을 이해해야 합니다.
해결책의 지형
문제에 대한 모든 가능한 해결책이 광활하고 언덕이 많은 지형의 한 지점이라고 상상해 보세요. 각 지점의 고도는 "비용"을 나타냅니다. 고도가 낮을수록 더 나은 해결책입니다. 목표는 전체 지도에서 가장 낮은 지점인 전역 최저점을 찾는 것입니다.
"탐욕스러운" 접근 방식과 그 결함
종종 언덕 오르기(hill-climbing)라고 불리는 간단한 알고리즘은 임의의 지점에서 시작하여 항상 내리막길로 이동합니다. 이는 즉각적인 개선을 가져오는 움직임만 수용하기 때문에 "탐욕스러운" 접근 방식입니다.
문제는 이 방법이 발견하는 첫 번째 계곡, 즉 지역 최저점에 갇히게 된다는 것입니다. 이 방법은 다음 언덕 너머에 훨씬 더 깊은 계곡, 즉 전역 최저점이 존재하는지 알 방법이 없습니다.
시뮬레이티드 어닐링이 더 나은 경로를 찾는 방법
시뮬레이티드 어닐링은 무작위성의 통제된 요소를 도입하여 이러한 지역 함정에서 벗어날 수 있도록 함으로써 이러한 한계를 극복합니다.
영감: 물리적 어닐링
야금학에서 금속을 가열하면 원자가 자유롭게 움직일 수 있는 충분한 에너지를 얻어 최적이 아닌 결함 있는 구조에서 벗어날 수 있습니다. 금속이 천천히 냉각됨에 따라 원자는 고도로 정렬되고 강한 결정 격자, 즉 최소 에너지 상태로 정착할 시간을 갖습니다.
알고리즘: 제어 노브로서의 온도
시뮬레이티드 어닐링은 온도 매개변수를 도입하여 이 개념을 채택합니다. 이것은 물리적 온도가 아니라 알고리즘의 동작을 제어하는 변수입니다.
알고리즘은 고온에서 시작합니다. 이 상태에서 알고리즘은 뜨거운 금속의 활기찬 원자처럼 해결책 지형을 적극적으로 탐색합니다. 현재 위치보다 나쁜 움직임을 수용할 확률이 높습니다. 이것이 핵심입니다. "나쁜" 움직임을 하는 것이 지역 최저점에서 벗어날 수 있게 해줍니다.
냉각 일정
알고리즘이 실행됨에 따라 냉각 일정에 따라 온도가 점차 낮아집니다. 온도가 낮아질수록 알고리즘은 더 나쁜 해결책을 수용할 가능성이 점점 줄어듭니다.
결국, 매우 낮은 온도에서는 알고리즘이 간단한 언덕 오르기 방법처럼 작동하여 개선 사항만 수용하고 바라건대 전역 최저점에서 위치를 미세 조정합니다.
트레이드오프 이해
다른 강력한 도구와 마찬가지로 시뮬레이티드 어닐링은 보편적인 해결책이 아닙니다. 그 한계를 이해하는 것이 효과적으로 사용하는 데 중요합니다.
강점: 지역 최저점 탈출
주요 장점은 많은 지역 최저점을 가진 복잡하고 비볼록한 지형을 탐색하는 능력입니다. 탐욕스러운 알고리즘이 지속적으로 실패하는 문제의 경우 시뮬레이티드 어닐링은 탁월한 선택입니다.
약점: 매개변수 튜닝이 중요
알고리즘의 성능은 냉각 일정에 매우 민감합니다. 너무 빨리 냉각되면 어쨌든 지역 최저점에 갇힐 수 있습니다("급랭"). 너무 느리게 냉각되면 해결책을 찾는 데 비현실적인 시간이 걸릴 수 있습니다. 올바른 일정을 찾는 데는 종종 실험이 필요합니다.
한계: 확률적 방법
시뮬레이티드 어닐링은 절대적으로 가장 좋은 해결책(전역 최저점)을 찾을 것이라고 보장하지 않습니다. 이는 합리적인 시간 내에 매우 좋은 해결책을 찾도록 설계된 휴리스틱입니다. 항상 최적이 아닌 상태에 정착할 통계적 가능성이 있습니다.
문제에 대한 올바른 선택
이 지침을 사용하여 시뮬레이티드 어닐링이 최적화 작업에 적합한 접근 방식인지 결정하십시오.
- 많은 함정(지역 최저점)이 있는 복잡한 문제를 해결하는 데 주로 초점을 맞춘다면: 시뮬레이티드 어닐링은 특히 외판원 문제(Traveling Salesperson Problem) 또는 회로 기판 배치와 같은 고전적인 문제에 가장 적합한 도구 중 하나입니다.
- 최대 속도로 증명 가능한 최적의 해결책을 찾는 데 주로 초점을 맞춘다면: 선형 프로그래밍 또는 표준 탐욕스러운 접근 방식과 같은 더 빠르고 결정론적인 알고리즘으로 해결할 수 있을 만큼 문제가 충분히 간단한지 (예: 볼록한지) 먼저 확인해야 합니다.
궁극적으로 시뮬레이티드 어닐링은 더 간단한 방법이 실패하는 경우 광대하고 어려운 탐색 공간을 탐색하여 고품질 해결책을 찾는 강력한 프레임워크를 제공합니다.
요약표:
| 특징 | 설명 |
|---|---|
| 영감 | 야금학적 어닐링 과정 (가열 및 서서히 냉각) |
| 핵심 강점 | 지역 최저점에서 벗어나 전역 최적점 찾기 |
| 핵심 매개변수 | 온도 및 냉각 일정 |
| 가장 적합한 경우 | 많은 지역 함정이 있는 복잡한 최적화 문제 |
| 한계 | 확률적; 신중한 매개변수 튜닝 필요 |
KINTEK으로 연구 개발 최적화
재료 과학, 화학 공학 또는 데이터 분석에서 복잡한 최적화 문제를 해결하고 계십니까? 시뮬레이티드 어닐링의 원리는 실제 열 과정에서 영감을 얻었으며, 실험실에서 이러한 과정을 정밀하게 제어하는 것이 중요합니다.
KINTEK은 연구 개발에 필수적인 균일한 가열 및 제어된 냉각을 제공하는 고급 오븐 및 용광로를 포함한 고품질 실험실 장비 전문 기업입니다. 새로운 재료를 개발하든 계산 실험을 수행하든, 신뢰할 수 있는 장비는 정확한 결과의 기초입니다.
지금 바로 전문가에게 문의하여 최적화 워크플로를 향상하고 획기적인 결과를 달성할 완벽한 실험실 솔루션을 찾아보십시오.
시각적 가이드